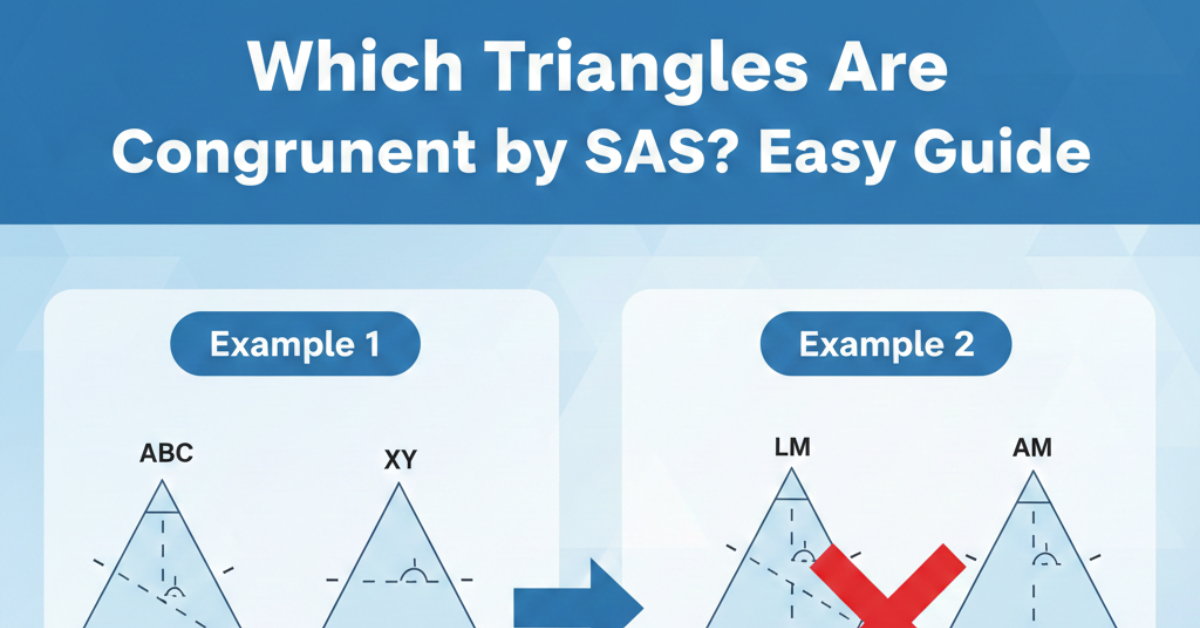
Geometry gets a lot easier once you understand triangle congruence rules. One of the most important—and commonly tested—is Side-Angle-Side (SAS). If you’ve ever wondered which pair of triangles can be proven congruent by SAS, this guide will break it down in plain language with visual explanations, examples, and practical tips.
Let’s make SAS simple and crystal clear.
What Does SAS Congruence Mean?
-
Two sides of one triangle match the length of two sides of another triangle.
-
The angle between those two sides (called the included angle) is equal in both triangles.
If these three elements match, the triangles are exactly the same size and shape—even if they’re rotated or flipped.
Key idea:
It must be the included angle. If the angle is not between the two given sides, SAS does not apply.
Which Pair of Triangles Can Be Proven Congruent by SAS?
A pair of triangles can be proven congruent by SAS only if:
-
Side A = Side A
-
Side B = Side B
-
The angle between those sides = the corresponding included angle
Example
Triangle 1:
-
AB = 6 cm
-
AC = 8 cm
-
∠A = 40°
Triangle 2:
-
DE = 6 cm
-
DF = 8 cm
-
∠D = 40°
Since the angle is between the two equal sides in both triangles, these triangles are congruent by SAS.
How to Identify SAS in a Problem
Use this quick checklist:
Step-by-Step Method
-
Mark the given sides
-
Check if two pairs of sides are equal
-
Locate the angle
-
Ask: Is the angle between those two sides?
If yes → SAS works
If no → Look for another rule (SSS, ASA, AAS, etc.)
Included Angle vs. Non-Included Angle
Included Angle (Correct for SAS)
The angle is between the two known sides.
Non-Included Angle (Not SAS)
“If the given sides do not include the angle, the situation forms an SSA case, which may not guarantee congruence; this is called the ambiguous case.”
Real-World Example of SAS
Think of building a triangular frame:
-
Two metal rods have fixed lengths.
-
The hinge between them locks at a specific angle.
Once those two sides and the included angle are fixed, the triangle’s shape is locked. No other shape is possible—that’s exactly why SAS proves congruence.
Common Mistakes to Avoid
-
Using SSA and calling it SAS
-
Ignoring whether the angle is included
-
Matching the wrong corresponding sides
-
Assuming triangles are congruent just because they “look similar”
Pro tip: Always label corresponding vertices before making a conclusion.
SAS vs Other Triangle Congruence Rules
| Rule | What You Need |
| SSS | Three equal sides |
| SAS | Two sides + included angle |
| ASA | Two angles + included side |
| AAS | Two angles + non-included side |
| HL | Right triangles only |
Knowing when to use SAS helps you solve proofs faster and avoid unnecessary steps.
Practice Scenario
Which pair is congruent by SAS?
-
Triangle A: sides 5 cm and 7 cm, angle between = 60°
-
Triangle B: sides 5 cm and 7 cm, angle between = 60°
Answer: Congruent by SAS.
If the 60° angle does not fall between the 5 cm and 7 cm sides, the SAS rule does not apply.
FAQs
1. What does SAS stand for in geometry?
Side–Angle–Side, meaning two sides and the included angle are equal.
2. Why must the angle be included?
Because the included angle fixes the triangle’s shape. Without it, multiple triangles could exist.
3. Can SSA prove congruence?
No. SSA is the ambiguous case and does not guarantee congruence.
4. How can I tell if angles are included?
Check whether the two given sides form the angle.
5. Do people use SAS in real life?
Yes. Engineering, construction, and design use SAS principles to ensure accurate shapes.
Conclusion
Any pair that has two corresponding sides equal and the included angle between them equal. When an angle sits between the matching sides, it locks the triangles into the same shape.
Master this rule, and geometry proofs become far less intimidating. Next, try identifying SAS in practice problems or explore related congruence rules like SSS and ASA to strengthen your skills.